La tecnica della X non è immediata da capire ma, una volta che avremo
imparato a usarla, ci aiuterà a eliminare numerosi candidati in situazioni
altrimenti difficili da risolvere. È una tecnica da esperti quindi non
scoraggiamoci se all’inizio dobbiamo pensarci un po’: basta prenderci l’abitudine
per avere nel nostro arsenale un ottimo strumento.
Prima di poterla applicare, dovremo inserire nella nostra griglia del Sudoku
tutti i possibili candidati di ogni cella. In ogni casella non risolta, cioè,
segneremo a matita tutti i numeri che non vengono esclusi dalla loro presenza in
caselle vicine all’interno dello stesso riquadro, della stessa riga o della
stessa colonna.
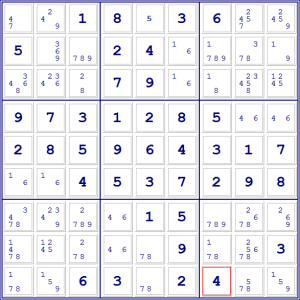
Per esempio, nello schema qui sotto abbiamo inserito tutti i candidati.
In questa situazione è difficile proseguire usando i metodi di base che si
applicano a una sola riga, a un solo riquadro o a una sola colonna. Cercheremo
quindi di lavorare su un’area più ampia. La base della tecnica della X è
cercare un numero che si trovi ripetuto quattro volte in angoli opposti formando
un quadrato. In due di questi casi (i due numeri sulla stessa riga o i due sulla
stessa colonna) i numeri ripetuti devono essere gli unici candidati per quella
riga o colonna. Sembra difficilissimo se non lo visualizziamo ma osservando con
un po’ di attenzione l’esempio qui sotto diventerà tutto più chiaro.
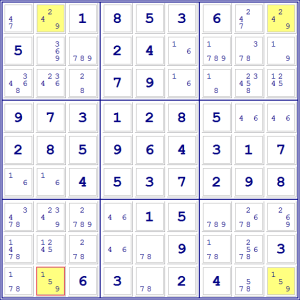
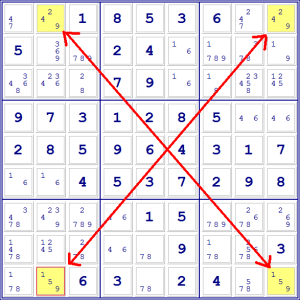
Per esempio, in questo caso il 9 si trova nella seconda e nell’ultima
colonna sia nella prima sia nell’ultima riga. In pratica i quattro 9 formano
un quadrato. Inoltre, non ci sono altri 9 né nella prima riga né nell’ultima,
quindi due dei quattro 9 sono candidati unici. Abbiamo quindi una situazione a
cui si può applicare la tecnica della X.
Non sappiamo ancora dove siano in realtà i 9, ma per forza ce ne deve essere
uno nella prima riga e uno nell’ultima.
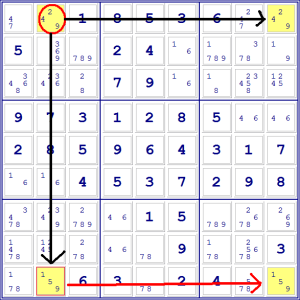
Proviamo a capire cosa succederebbe agli altri 3 candidati se presupponessimo
che il primo è al suo posto. Per facilitarci il compito, prendiamo due matite
colorate. Nel nostro caso ne abbiamo presa una rossa e una nera. Tracciamo delle
frecce rosse verso le caselle che sarebbero confermate se il nostro 6 in B1
fosse giusto, e delle frecce nere verso le caselle che non potrebbero contenere
il candidato.
Dato che non possono esserci due 9 nella stessa riga, quello in I1 andrebbe
eliminato.
Allo stesso modo, dato che non possono esserci due 9 nella stessa colonna,
quello in B9 andrebbe eliminato.
D’altra parte, una volta eliminato quest’ultimo, il 9 in I9 deve essere per
forza giusto, perché è rimasto l’unico candidato nella riga.
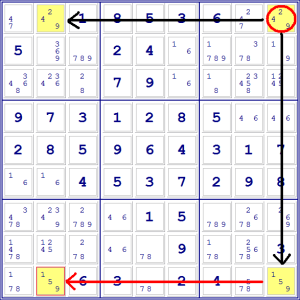
D’altra parte, supponiamo che il 9 in I1 sia giusto.
Dato che non possono esserci due 9 nella stessa riga, quello in B1 andrebbe
eliminato.
Allo stesso modo, dato che non possono esserci due 9 nella stessa colonna,
quello in I9 andrebbe eliminato.
D’altra parte, una volta eliminato quest’ultimo, il 9 in B9 deve essere per
forza giusto, perché è rimasto l’unico candidato nella riga.
In pratica, qualunque sia il 9 giusto, determina automaticamente che sia
corretto anche quello a lui opposto in diagonale. Se uniamo i candidati che sono
giusti insieme formiamo una X: è lei a dare il nome a questa tecnica di
soluzione.
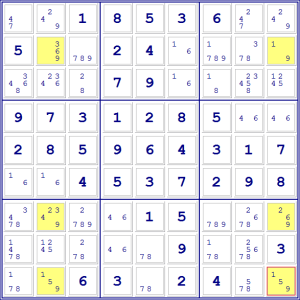
Qualunque sia la coppia di 9 giusta, quindi, ci sarà sicuramente un 9 nella
seconda colonna e uno nell’ultima.
Possiamo allora eliminare tutti gli altri 9 in queste due colonne.
In questo modo escludiamo quattro candidati nelle caselle. Un aiuto
considerevole in un Sudoku di difficoltà avanzata!














Commenta via Facebook