17 indizi: pochi ma buoni!

Lo schema qui di fianco possiede solo 17 indizi. Pensate non bastino? Vi sbagliate!

17 sono pochi, ma sufficienti perché lo schema abbia una sola soluzione.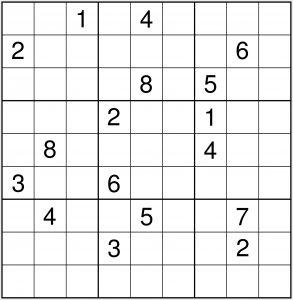

Questo numero limite è stato confermato da uno studio condotto da un gruppo di ricerca dell’University College di Dublino, guidato dal professor Gary McGuire. Per giustificare il numero 17, il team ha “semplicemente” raccolto tutti gli schemi possibili con 16 indizi (ossia quasi 5,5 miliardi di griglie!) e, dopo un lavoro computazionale enorme affidato ad uno specifico program-solver, è stato scoperto che in nessun caso bastano 16 indizi per ottenere un’unica soluzione.

Così, finalmente, a gennaio del 2012, hanno ufficialmente dichiarato che 17 è il numero minimo di indizi. Pare che, oltre a soddisfare la curiosità degli amanti del sudoku, l’algoritmo realizzato dal team troverà applicazione in tutti quei campi in cui è necessario esaminare enormi quantità di dati.

Ad ogni modo, dopo lo studio condotto dal professor McGuire, anche un altro matematico si è dedicato a questa ricerca: Ed Russel. Secondo questo studioso, esistono solamente 18 sudoku simmetrici con 17 candidati iniziali.

Avete voglia di misurarvi con questo schema estremo? Stampate la griglia e mandateci una email con la soluzione e i vostri commenti all’indirizzo posta@settimanasudoku.it!