La tecnica XY wing è più complessa da spiegare che da applicare. È una tecnica
da esperti quindi non scoraggiamoci se dobbiamo leggere un paio di volte la
spiegazione per orientarci: una volta che avremo imparato a usarla potremo
eliminare candidati in situazioni altrimenti bloccate.
Prima di poterla applicare, dovremo inserire nella nostra griglia del Sudoku
tutti i possibili candidati di ogni cella. In ogni casella non risolta, cioè,
segneremo a matita tutti i numeri che non vengono esclusi dalla loro presenza in
caselle vicine all’interno dello stesso riquadro, della stessa riga o della
stessa colonna.
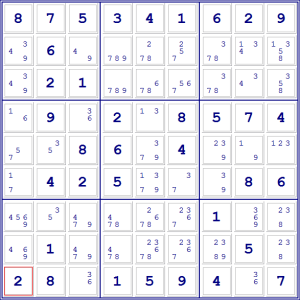
Per esempio, nello schema qui sotto abbiamo inserito tutti i candidati.
In questa situazione è difficile proseguire usando i metodi di base che si
applicano a una sola riga, a un solo riquadro o a una sola colonna. Cercheremo
quindi di lavorare su un’area più ampia. La base della tecnica XY è cercare
tre numeri che si trovino ripetuti, mescolati in coppie diverse, in tre celle
collegate. Chiamiamo i numeri X, Y e Z. Le tre coppie, per essere diverse,
dovranno essere XY (che da il nome alla tecnica) XZ e YZ. Le celle possono
essere collegate perché si trovano nella stessa riga, nella stessa colonna o
nello stesso riquadro.
Sembra molto complesso ragionando in astratto con le lettere ma se
osserveremo con un po’ di attenzione l’esempio qui sotto e i suoi numeri
diventerà tutto più chiaro.
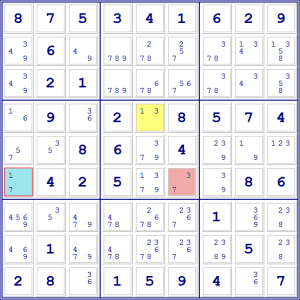
Per esempio, in questo caso i nostri tre numeri sono 1 (X) 3 (Y) e 7 (Z). La
coppia 1-3 è quindi XY, mentre 1-7 è XZ e 3-7 è YZ. Le loro celle sono
collegate perché XY e YZ si trovano nello stesso riquadro (quello centrale),
mentre YZ e XZ si trovano nella stessa riga (la sesta). Possiamo quindi
applicare la tecnica XY. Per comodità diamo alle tre caselle colori diversi, in
modo da identificarle più facilmente.
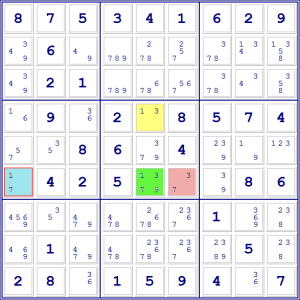
Lo scopo di questa tecnica non è risolvere le tre caselle in esame, ma
eliminare dei candidati nelle caselle in cui i due collegamenti si incrociano:
nel nostro caso, la casella del riquadro centrale che appartiene alla sesta
riga, che chiameremo il nostro bersaglio e nel nostro esempio coloreremo di
verde.
Il numero in comune tra il bersaglio, la casella gialla e la casella azzurra è
l’1, la nostra X.
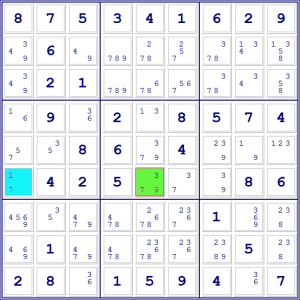
Supponiamo che l’1 sia giusto in nella casella gialla: in questo caso
potremo eliminarlo come candidato nel bersaglio, perché non possiamo avere due
1 nella stessa colonna.
Supponiamo invece che l’1 sia giusto in quella azzurra: anche in questo
caso potremo eliminarlo come candidato nel bersaglio, perché non possiamo avere
due 1 nella stessa riga.
In entrambi i casi, quindi, possiamo eliminare l’1 come candidato nel
bersaglio.
Abbiamo eliminato un solo candidato ma è un importante passo avanti. A questo
punto, infatti, l’1 nella casella azzurra rimane l’unico candidato per la
riga, quindi deve essere giusto e questa casella a sua volta ne risolverà
altre… Abbiamo sbloccato una situazione molto complessa.
https://youtu.be/Jq9wxsZ799s














Commenta via Facebook