Chiariamo subito che questa non è una vera e propria tecnica risolutiva. Potremmo chiamarla un’astuzia, ma può capitare di imbattersi in situazioni di questo tipo e dunque, perché non trarne profitto per velocizzare la soluzione dello schema?
Dando per scontato che il problema proposto non contiene errori e ha una soluzione unica, allora si possono riconoscere situazioni non compatibili con quella della soluzione. In altre parole, certi numeri non possono andare in certe caselle perché altrimenti il problema non sarebbe univoco, ma avrebbe una doppia soluzione. Questo stratagemma risolutivo è in realtà applicabile anche a molti altri tipi di rompicapo, come per esempio il Kakuro.
Ma come si fa ad essere sicuri che il problema proposto sia davvero esatto?
Beh, stiamo parlando di Settimana Sudoku! Tutti gli schemi di Settimana Sudoku sono di altissima qualità e a prova di errore, puoi applicare – se ti va – il criterio di univocità con tutta tranquillità.
Sostanzialmente ai 4 vertici di un rettangolo non possono mai stare le stesse coppie di numeri, perché altrimenti si formerebbe un “loop” con due possibili soluzioni.
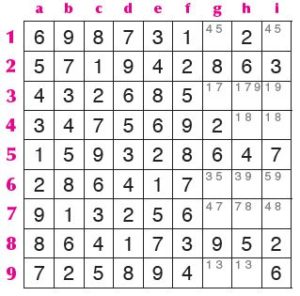
Consideriamo la seguente figura come se fosse parte di un sudoku completo e quindi sicurmanete univoco. Vediamo subito che ha le stesse coppie di candidati nelle caselle b2–b3–h3.
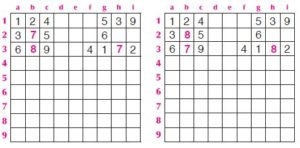
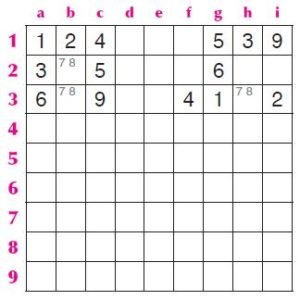 Ora se anche nella casella h2 ci fosse un 7 o un 8, il sudoku ammetterebbe due soluzioni, perché si sarebbe formato un rettangolo con ai vertici le stesse coppie, come si vede facilmente dalle seguenti figure.
Ora se anche nella casella h2 ci fosse un 7 o un 8, il sudoku ammetterebbe due soluzioni, perché si sarebbe formato un rettangolo con ai vertici le stesse coppie, come si vede facilmente dalle seguenti figure.
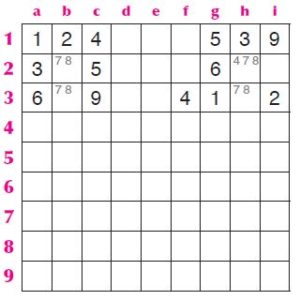
In realtà nello schema i possibili candiati per la casella h2 sono tre: 4, 7 e 8, infatti quella casella già “vede” tutti gli altri numeri: 1, 2, 3, 5, 6 e 9.
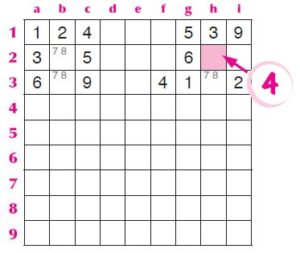
Ma abbiamo visto che il 7 e l’8 non ci possono andare perché altrimenti lo schema avrebbe una doppia soluzione… quindi non può andarci che il 4.
Alcune persone sono restie a usare questo tipo di pensiero, perché in realtà si tratta di una sorta di logica al contrario basata sul presupposto che il gioco proposto sia corretto invece che arrivare alla soluzione in maniera “diretta”. A tutti gli effetti può essere considerata una scorciatoia che dà per scontata la correttezza del rompicapo. Tu regolati come credi.
BUG+1
Alla stessa famiglia di “stratagemmi” appartiene la tecnica nota come Bug+1, applicabile molto raramente e solo in situazioni estreme. Prima di spiegarla dobbiamo enunciare il Teorema dello stallo perfetto o Bug. Se ti trovi in una situazione in cui in TUTTE le caselle libere di un Sudoku sono possibili esattamente due candidati, significa che il problema è sbagliato: o la soluzione è impossibile o non è unica. Per applicare la tecnica Bug+1, dobbiamo trovarci invece in una situazione in cui tutte le caselle libere tranne una hanno due candidati e quella che fa eccezione ne ha tre: così è possibile evitare il “bug”. In questo caso risulta che uno dei tre candidati della casella che ne ha tre, compare necessariamente tre volte nella sua riga, nella sua colonna e nel suo settore. Se ora escludessimo quel candidato dai tre possibili nella casella, tutte le caselle avrebbero solo due candidati e di conseguenza il gioco sarebbe errato. Dunque quello è proprio il numero da inserire in quella casella.
Quando tutte le caselle libere contengono due candidati tranne una che ne contiene tre, in tale casella va inserito
il candidato che compare tre volte nella stessa riga, colonna e settore.
Ecco uno schema in cui ci troviamo in una situazione Bug+1.
In quattordici delle quindici caselle libere ci sono due candidati, nella quindicesima (h3) ce ne sono tre e il numero presente tre volte nella riga 3, nella colonna h e nel settore III è 1. Se escludiamo l’1 da h3 ci troviamo in tutte le caselle con due candidati ed entriamo nel caso dello stallo perfetto: in h3 pertanto dobbiamo inserire l’1 per evitare il “bug”.














Commenta via Facebook