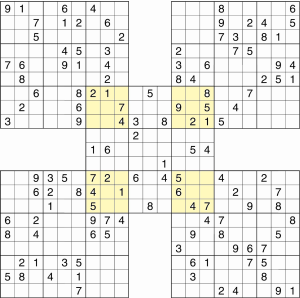
In questa variante del Sudoku, cinque griglie 9 x 9 sono unite a forma di croce. La griglia centrale condivide un riquadro con ciascuna delle 4 griglie esterne.
Ecco un esempio:
Attenzione però, perché, a parte i riquadri evidenziati in giallo nel disegno, gli indizi dei vari schemi sono “a se stanti” e non influenzano gli altri. Per esempio, gli indizi delle zone 1,2,3 (in verticale) dello schema in alto a destra, influenzano solo il riquadro in alto a destra dello schema centrale e nessun altro. È facile confondersi mentre si affronta lo schema la prima volta.
In pratica sono 5 sudoku del tutto separati, se non per i riquadri evidenziati in giallo in questo schema, che sono comuni a due sudoku.
Le regole sono del tutto analoghe a quelle del Sudoku: ogni griglia si divide in righe, colonne e riquadri 3×3. All’interno di ciascuna riga, colonna o riquadro si devono trovare tutti i numeri dall’1 al 9, senza mai ripetersi.
Naturalmente un Samurai è più lungo da risolvere di un Sudoku tradizionale (in fondo, dobbiamo risolvere 5 griglie e non una!) ma non facciamoci spaventare. Per certi versi è persino più semplice. Per i riquadri comuni a due griglie (evidenziati in giallo nel nostro schema), abbiamo infatti più indizi a nostra disposizione, perché si sommano gli indizi presenti nei due schemi.
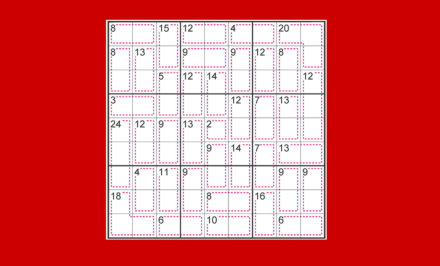
Vediamo, per esempio, l’ultimo riquadro del primo schema in alto a sinistra, che è anche il primo riquadro dello schema centrale.
Inseriamo tutti i candidati, cioè tutti i numeri che possono essere inseriti nelle caselle perché non sono già presenti nelle colonne, nelle righe o nei riquadri.
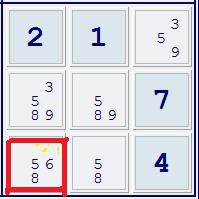
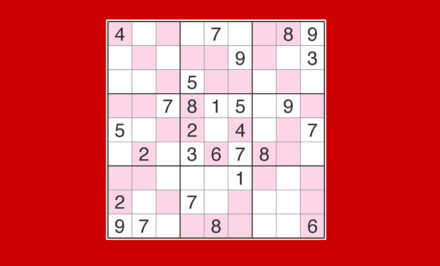
Vedendo il riquadro solo come parte della prima griglia, l’unica cosa che notiamo è che il 6 in G9 (riquadrato in rosso nella figura) è l’unico candidato nel riquadro, quindi deve essere per forza giusto. Nessun’altra soluzione balza all’occhio guardando solo il primo schema, ma abbiamo un aiuto anche dallo schema centrale. Lo stesso riquadro compare infatti anche all’interno di questa griglia, solo che invece essere l’ultimo è il primo. Guardiamo il nostro riquadro al suo interno, considerando anche gli altri riquadri sulla stessa riga.
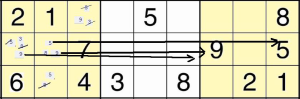
Osserviamo la casella centrale del nostro riquadro, che ora (rispetto a righe e colonne della griglia centrale) inizia nella posizione AI. Se osserviamo i candidati in B2, notiamo che due su tre (il 5 e il 9) non sono validi perché compaiono già nella stessa riga (vedi frecce). La soluzione di B2 è quindi 8. Possiamo allora togliere gli altri 8 come candidati nel riquadro. Dato che in B3 c’erano solo 2 candidati, la sua soluzione è 5. Possiamo quindi togliere anche i 5 come candidati dalle celle di questo riquadro. In A2 sono rimasti dunque due candidati: 3 e 9. Il 9 però è già presente nella riga (vedi freccia), quindi lo possiamo eliminare e lasciare solo il 3. A questo punto possiamo togliere il 3 come candidato in C1 e risolvere anche quella casella, che rimane 9. Abbiamo risolto il riquadro!
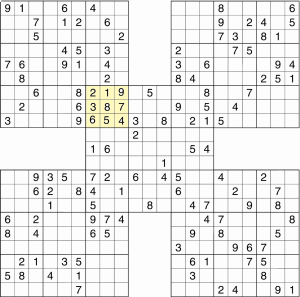
Ora possiamo concentrarci sulla griglia centrale, per cui abbiamo molti dati e, sfruttando le tecniche classiche del Sudoku (spiegate nell’Università del Sudoku su questo stesso sito) oltre alle indicazioni date dalle righe e colonne in comune con altre griglie, l’avremo presto completata. La griglia centrale completata, a sua volta ci darà indizi preziosi per risolvere le altre e presto il nostro Samurai sarà finito!












Commenta via Facebook