Per posizioni proibite di gruppi (Hidden Subsets)

La tecnica delle posizioni proibite di gruppi è molto utile e ci può levare
dai guai nei Sudoku difficili. È però una tecnica avanzata e per poterla
applicare è utile saper già usare bene l’eliminazione di gruppi. Se non
abbiamo ancora imparato quella tecnica, quindi, è consigliabile studiarla per
prima.

La tecnica delle posizioni proibite di gruppi ci permette di escludere la
presenza di alcuni gruppi di numeri (che possono essere costituiti da due, tre o
quattro numeri) da determinate caselle.

Prima di poterla applicare, dovremo inserire nella nostra griglia del Sudoku
tutti i possibili candidati di ogni cella. In ogni casella non risolta, cioè,
segneremo a matita tutti i numeri che non vengono esclusi dalla loro presenza in
caselle vicine all’interno dello stesso riquadro, della stessa riga o della
stessa colonna.

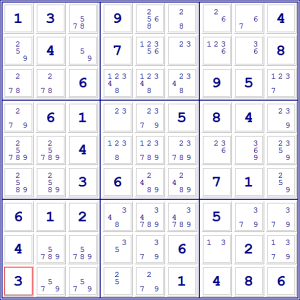
Per esempio, nello schema qui sotto abbiamo inserito tutti i candidati.

Cerchiamo ora di identificare un’area, che può essere una colonna, una riga o
un gruppo di riquadri, per vedere se ce n’è una che contiene solo due volte
una coppia di numeri (prendiamo come esempio una coppia ma possono essere anche
tre numeri presenti in tre celle o quattro numeri presenti in quattro). Nel
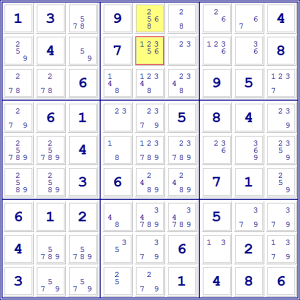
nostro caso, troviamo questa situazione nella quinta colonna. La coppia 5-6,
infatti, compare come candidato in E1 ed E2 (indicando con le lettere le colonne
e con i numeri le righe). In nessun altro punto possono comparire né il 5 né
il 6.

Non sappiamo ancora in quale casella sia il 5 e in quale sia il 6 ma siamo
sicuri che in queste due posizioni può andare solo uno di questi due numeri.
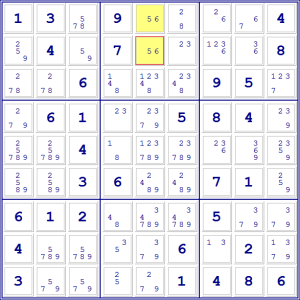
Possiamo quindi eliminare tutti gli altri candidati dalle due caselle.

In questo modo siamo rimasti con due soli candidati nelle caselle. Un bel passo
avanti!