Questa variante è una sorta di incrocio fra il sudoku classico e il kakuro.
Nel sudoku killer vi sono una serie di “zone” individuate dal bordo a puntini e da un numerino in alto a sinistra: sommando i numeri contenuti in ciascuna zona (che devono essere tutti diversi) si ottiene proprio quel numerino.
Valgono tutte le regole (e le tecniche) del sudoku, ma soprattutto per risolverlo sono utili le tecniche (e le tabelle!) che abbiamo sviluppato per il kakuro, infatti le “zone numeriche” corrispondono in qualche modo alle “definizioni” del kakuro. Soprattutto all’inizio, perché in generale non vi sono indizi nello schema.
L’incrocio delle due serie di tecniche dà luogo a situazioni piuttosto interessanti e anche – bisogna ammetterlo – spesso complesse. In altre parole, il sudoku killer è una variante comunque impegnativa, anche quando gli schemi sono accessibili.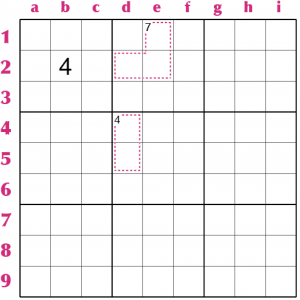
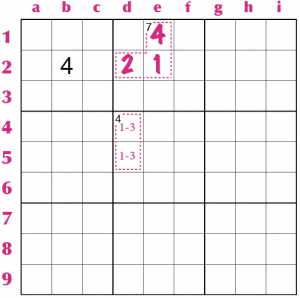
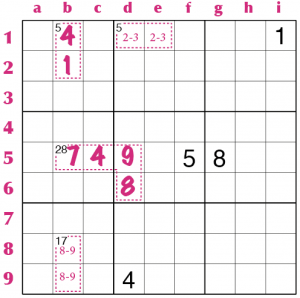
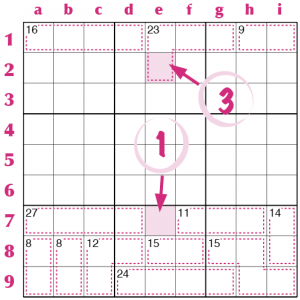
Consideriamo il 7 in tre caselle (o 7[3], per usare la stessa notazione sviluppata per il kakuro) da ottenere nelle 3 caselle d2, e1 ed e2; deve contenere le cifre 1, 2 e 4, come si può desumere dalle tabelle del kakuro (nelle pagine precedenti); ma il 4 non può stare nella riga 2 perché già presente in b2, dunque deve stare in e1: in d2 ed e2 ci staranno 1 e 2, ma in che ordine? Se consideriamo il 4[2] da ottenere nelle caselle d4 e d5, sappiamo che deve essere composto da 1 e 3 e dunque l’1 c’è già nella colonna d e deve andare in e2, mentre in d2 ci andrà il 2.
Consideriamo un altro esempio: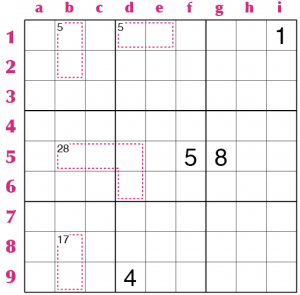
Dalla Tabella Possibili Somme, sappiamo che il il 5[2] può essere composto solo da 1–4 e da 2–3. Visto che nella riga 1 c’è già un 1, il 5[2] in d1–e1 non può che essere un 2–3, anche se non sappiamo in quale casella va il 2 e in quale va il 3. Se consideriamo ora l’altro 5[2] in b1–b2, notiamo che nella casella b1 non può andare l’1, ma non possono andare nemmeno il 2 e il 3, che costituiscono una “coppia” vincolata alle caselle d1 ed e1. Dunque in b1 ci sarà necessariamente un 4 e in b2 un 1.
Ma attenzione, le zone numeriche del killer non stanno necessariamente dentro un singolo settore dello schema di sudoku, possono invece debordare in due o più settori. E in ogni caso le cifre dentro ogni singola zona non devono ripetersi, anche se appartengono a settori diversi. Consideriamo il 28[4] che sta fra i settori IV e V. Può essere composto da 4–7–8–9 oppure 5–6–8–9; ma notiamo che in nessuna delle sue caselle può starci un 5 e quindi il gruppo deve essere 4–7–8–9. L’unica casella dove può andare il 4 è c5, poi l’8 va in d6 (c’è già nella riga 5), resta la “coppia” 7–9 nelle caselle b5 e d5; ma il 17[2] in b8–b9, dirime il dubbio: il 9 non può stare nella colonna b perché c’è già come coppia nel 17[2] che è 8–9, quindi in b5 va il 7 e in d5 va il 9.
Tecnica degli “Interni-esterni”
Questa è una tecnica molto simpatica che si basa sul fatto che la somma dei numeri da 1 a 9 è sempre e comunque 45. Il totale di ogni riga è 45, il totale di ogni colonna è 45, il totale di ogni settore è 45.
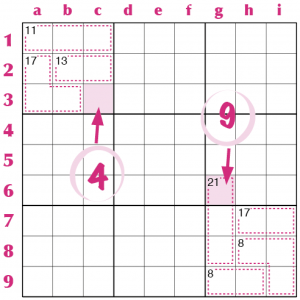
Nel settore I le zone numeriche coprono internamente 8 delle 9 caselle, dando un totale di 11+13+17=41. L’unica casella “interna” di quel settore, nel nostro caso la casella c3, deve essere il complemento a 45, cioè ciò che manca per arrivare a 45; e ciò indipendentemente dalla zona numerica a cui quella casella appartiene.
All’opposto può essere che un gruppo di zone numeriche copra tutto un settore più una casella esterna, come nel settore IX della stessa figura. In questo caso il totale sarà più alto di 45 e sarà proprio la differenza con 45 a determinare il valore della casella. Nel nostro caso 8+8+17+21= 54; 54-45=9 e dunque nella casella “esterna” ci va il 9. Naturalmente ci possono più caselle interne o esterne, ma spesso comunque ciò può tornare utile per la soluzione dello schema.
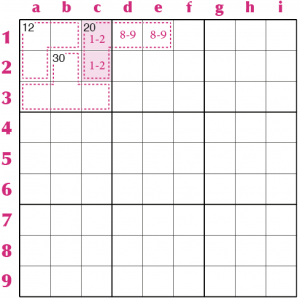
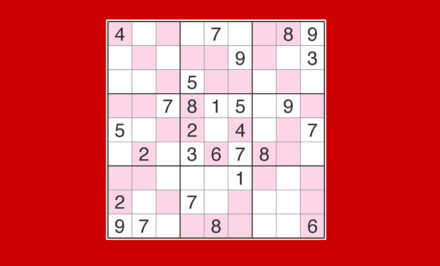
Le caselle c1–c2 sono “interne” e la loro somma è 3 (infatti 12+30=42 e 45-42=3), quindi devono essere una coppia 1-2, il che implica che le caselle d1–e1 sono un’altra coppia, 8-9, perché la loro somma è 17. Finora abbiamo ragionato su singoli settori, ma la tecnica delle caselle residue interne ed esterne si può anche applicare a gruppi di settori o righe o colonne, ogni volta insomma che una data area fa 45, o 90, o magari 135. Vediamo evidenziato qualche esempio.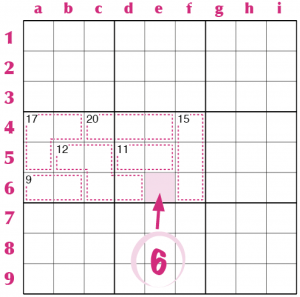
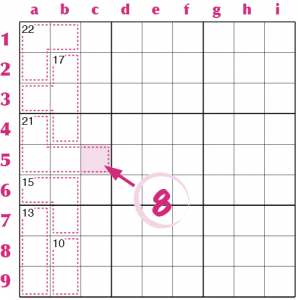
La somma di due settori è 90, la somma delle zone dà 84, dunque la casella interna scoperta è un 6.
La somma delle due colonne è 90, la somma delle zone è 98, dunque la casella esterna scoperta è un 8.
La somma della riga 1 è 45, la somma delle zone in alto è 48, dunque la casella esterna scoperta è un 3. La somma dei tre settori VII, VIII e IX è 135, la somma delle zone dà 134, dunque la casella interna scoperta è 1.













Commenta via Facebook