Il Kakuro è un gioco di logica combinatoria giapponese come il Sudoku e come quest’ultimo ha delle regole molto semplici ma per risolverlo servono ingegno e attenzione.
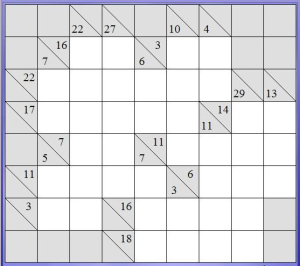
La griglia è composta di celle più scure inutilizzate, celle chiare vuote in cui scriveremo i numeri e caselle divise a metà in diagonale, con dei numerini scritti al loro interno che rappresentano la chiave della soluzione del Kakuro.
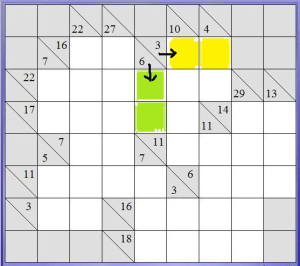
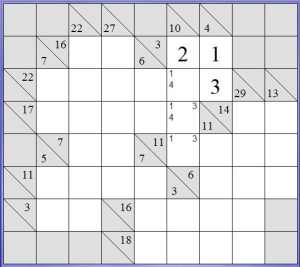
La griglia si può suddividere in blocchi: un blocco è la serie di caselle vuote che segue un indizio e finisce contro una casella grigia: può essere orizzontale (riga) o verticale (colonna). Nell’esempio in basso abbiamo evidenziato in giallo un blocco verticale e in verde uno orizzontale. Il nostro scopo è mettere un numero compreso tra 1 e 9 in ogni cella vuota, senza mai ripetere lo stesso numero in un blocco. La somma dei numeri contenuti in un blocco deve essere uguale al numerino che ha come indizio sopra (per le colonne) o sulla sua sinistra (per le righe). Quando la casella dell’indizio contiene due numeri, quello nel triangolino in alto è l’indizio della riga sulla sua sinistra, quello in basso è l’indizio della colonna sotto di esso, come indicano le frecce nere nell’immagine.
Come dicevamo, i numeri non si possono ripetere all’interno di un blocco. Un blocco, cioè, non può contenere due 3 o due 4, per esempio, ma solo numeri diversi tra loro.
Vediamo un esempio:
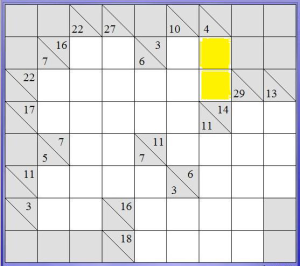
Nella colonna evidenziata, il nostro indizio è 4.
Sappiamo quindi che i numeri che vanno in quelle due celle devono avere come somma 4: potrebbero quindi essere: 1 +3, 3+1 o 2 +2. Possiamo subito scartare 2 + 2, perché un numero non può ripetersi all’interno della stessa riga o colonna.
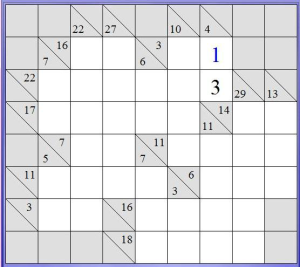
Dobbiamo solo stabilire in che ordine vanno l’1 e il 3. Per farlo guardiamo le righe a cui i numeri appartengono. La prima ci dà subito la nostra soluzione: è formata da due celle e il suo totale è 3, quindi non può contenere un 3. Dovrà contenere forzatamente il nostro 1.
Una volta inserito l’1, l’unico numero che possiamo inserire perché il totale della riga sia 3 è 2.
A questo punto possiamo scegliere come proseguire. Possiamo cercare altre caselle che hanno solo due possibili soluzioni (come 3=1+2 o 4=1+3), cercare di risolvere la colonna 10 o la riga 22 (per cui abbiamo già un numero inserito nello schema) o procedere metodicamente, inserendo i possibili candidati (con una tecnica analoga a quella usata nel Sudoku).
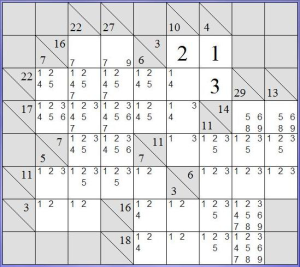
Per inserire i candidati, dobbiamo mettere in ogni cella tutti i numeri che potrebbero rappresentare la soluzione e che non compaiono già nella riga o nella colonna. Per esempio, se 4 celle devono formare il numero 10, nessuna di esse può contenere un numero più alto di 4 (altrimenti qualsiasi numero non ripetuto mettiamo nelle altre celle, il totale darà più di 10). Usiamo questa informazione per inserire i candidati della colonna H.
Procediamo allo stesso modo per inserire gli altri candidati: le prime volte che lo facciamo l’operazione richiede un po’ di tempo, ma ci si prende l’abitudine e, soprattutto, inserire i candidati rende molto più semplice la soluzione del Kakuro.
Ecco il nostro schema con tutti i candidati inseriti.
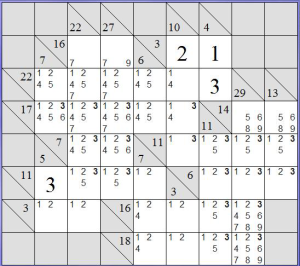
Con tutti i candidati inseriti, ci si aprono parecchie possibilità per proseguire. Per esempio, la colonna che comincia in B6 deve avere come totale 5. Dato che in una sola delle due caselle c’è il 3 come candidato (e gli unici numeri che possono dare 5 in due celle sono 3 e 2), deve essere per forza giusto.
Di conseguenza, in B7 deve esserci il 2 e, dato che la somma della riga è 3, in C7 deve esserci l’1.
A questo punto possiamo procedere a eliminare i candidati già presenti nella riga 6 e nella colonna B.
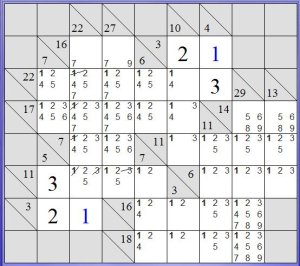
Anche questo ci dà nuovi indizi. Per esempio, E6 può essere un solo numero se facciamo i conti nella riga…
Proseguiamo così e, con un po’ di pazienza, presto il nostro Kakuro sarà risolto!
Trucchi utili
Se non vogliamo perdere tempo con l’aritmetica e dedicarci solo alla parte logica del Kakuro, possiamo usare la tabella qui sotto. Riporta tutte le possibili combinazioni che sommate danno un certo indizio.
Può essere utile inoltre ricordare un paio di regole sempre valide:
– le soluzioni di nove celle contengono sempre tutte le cifre da ‘1’ a ‘9’ e quindi la loro definizione sarà sempre “45”;
– le soluzioni di otto celle avranno come definizione necessariamente 45 meno il valore della cifra mancante;














Commenta via Facebook