La tecnica delle concatenazioni forzate è riservata agli esperti e richiede
una serie di ragionamenti piuttosto lunga e complessa. Ci può però risolvere
situazioni in cui non ci sono altre soluzioni possibili. Prima di studiarla
sarebbe opportuno avere già una buona dimestichezza con le altre tecniche
proposte nella nostra Università del Sudoku. Anche allora, dovremo armarci di
pazienza: ne vale la pena perché ci permetterà di risolvere anche i Sudoku
più difficili!
Prima di poter applicare questa tecnica, dovremo inserire nella nostra
griglia del Sudoku tutti i possibili candidati di ogni cella. In ogni casella
non risolta, cioè, segneremo a matita tutti i numeri che non vengono esclusi
dalla loro presenza in caselle vicine all’interno dello stesso riquadro, della
stessa riga o della stessa colonna.
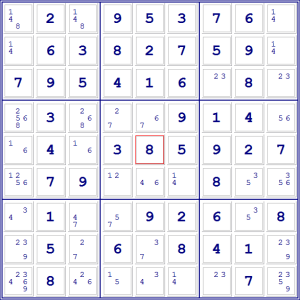
Per esempio, nello schema qui sotto abbiamo inserito tutti i candidati.
Per cercare di sbloccare questa situazione con il metodo delle concatenazioni
forzate dobbiamo individuare delle connessioni tra caselle che hanno solo due
candidati, in modo da poterne eliminare alcuni.
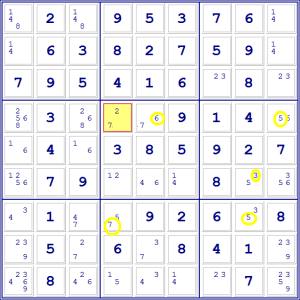
Decidiamo di partire dalla D4 (indicando con le lettere le colonne e con i
numeri le righe) che ha come candidati 2 e 7 e vediamo cosa succede alle altre
caselle se supponiamo che il valore corretto sia il 7. Indichiamo con un cerchio
giallo i candidati che vengono forzati da questa scelta.
Se il 7 in D4 è giusto, quello in E4 è forzatamente sbagliato, perché non
possiamo avere due 7 nello stesso riquadro. Di conseguenza è giusto il 6.
Questo però, significa che non può esserci un 6 nell’ultima colonna, perché
ne avremmo due nella stessa riga. Quindi in I4 andrà il 5. Dato che non possono
esserci due 5 nello stesso riquadro, possiamo toglierlo da H6. Qui rimane il 3.
Dato che non possono esserci due tre nella stessa colonna, possiamo eliminare il
3 da H7, dove rimane il 5. Dato che non possono esserci due cinque nella stessa
riga, possiamo eliminarlo da D7, dove rimane il 7.
Questo 7, però, è nella stessa colonna del 7 da cui siamo partiti. Non
possiamo avere due 7 nella stessa colonna, quindi la nostra scelta iniziale di
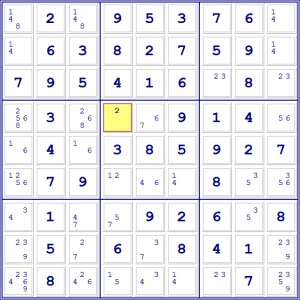
considerare giusto il 7 in D4 era sbagliata. Sappiamo quindi per certo che in D4
va il due.
La parte complicata di questa tecnica non è l’esecuzione ma la ricerca del
candidato che attiva la catena forzata. Potrebbero volerci diversi “passaggi”
per trovare quello giusto quindi, in caso di uno schema particolarmente
difficile, non scoraggiamoci e continuiamo a cercare.














Commenta via Facebook