La tecnica dell’area chiusa (o Swordfish) è riservata agli esperti ed è piuttosto
difficile da applicare. Ci può però risolvere situazioni in cui non ci sono
altre soluzioni possibili. La tecnica dell’area chiusa è un’estensione più
avanzata di quella della X. Prima di studiarla, quindi, dovremo saper usare bene
la tecnica della X. Anche quando siamo padroni della tecnica della X, ci vuole
un po’ di ragionamento per usare quella dell’area chiusa: non lasciamoci
scoraggiare!
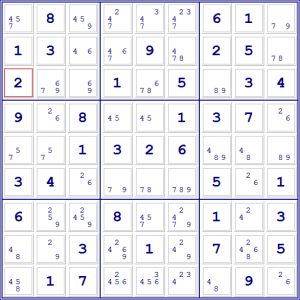
Prima di poterla applicare, dovremo inserire nella nostra griglia del Sudoku
tutti i possibili candidati di ogni cella. In ogni casella non risolta, cioè,
segneremo a matita tutti i numeri che non vengono esclusi dalla loro presenza in
caselle vicine all’interno dello stesso riquadro, della stessa riga o della
stessa colonna.
Per esempio, nello schema qui sotto abbiamo inserito tutti i candidati.
In questa situazione è difficile proseguire usando i metodi di base che si
applicano a una sola riga, a un solo riquadro o a una sola colonna. Cercheremo
quindi di lavorare su un’area più ampia. La base della tecnica dell’area
chiusa è cercare un numero che si trovi ripetuto sei o più volte in angoli
opposti formando una figura chiusa. Mentre nella tecnica della X cercavamo di
costruire un quadrato, in questo caso ci basta una qualsiasi figura, regolare o
irregolare, chiusa. Sembra difficilissimo se non lo visualizziamo ma osservando
con un po’ di attenzione l’esempio qui sotto diventerà tutto più chiaro.
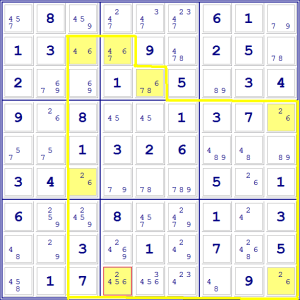
Per esempio, in questo caso unendo tutti i 6 evidenziati formiamo una figura
irregolare ma chiusa (ogni angolo che contiene un numero da determinare, cioè,
contiene un 6). Abbiamo quindi una situazione a cui si può applicare la tecnica
dell’area chiusa.
Non sappiamo dove siano in realtà i 6, ma per forza ce ne deve essere uno
nella seconda riga e abbiamo solo due caselle possibili.
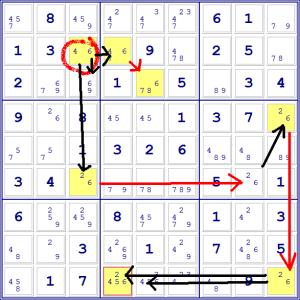
Proviamo a capire cosa succederebbe agli altri candidati se presupponessimo
che il 6 in C2 (indicando con le lettere le colonne e con i numeri le righe) è
al suo posto. Armiamoci di un po’ di pazienza e di due matite colorate. Nel
nostro caso ne abbiamo presa una rossa e una nera. Tracciamo delle frecce rosse
verso le caselle che sarebbero confermate se il nostro 6 in C2 fosse giusto, e
delle frecce nere verso le caselle che non potrebbero contenere il candidato.
Dato che non possono esserci due 6 nella stessa colonna, quello in C3 e quello
in C6 vanno eliminati.
Se eliminiamo questo candidato, però, il 6 in H6 deve essere per forza
giusto, altrimenti non ci sono sei nella riga.
Se quest’ultimo è giusto, non ci possono essere altri sei nel suo stesso
riquadro quindi possiamo eliminare anche il 6 in I4.
Quindi il 6 del secondo riquadro in basso deve forzatamente essere in I9
(altrimenti questa colonna non ha 6) e possiamo eliminare gli altri candidati
nella riga.
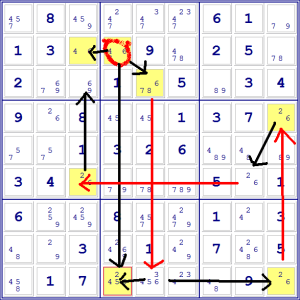
Immaginiamo ora che il 6 nella quarta colonna della seconda riga sia al posto
giusto.
Dato che non possono esserci due 6 nella stessa riga, quello in C3 andrebbe
eliminato.
Allo stesso modo, dato che non possono esserci due 6 nello stesso riquadro,
quello in E3 andrebbe eliminato.
D’altra parte, una volta eliminato quest’ultimo, il 6 in E9 deve essere per
forza giusto, perché è rimasto l’unico candidato nella colonna.
Se questo 6 è giusto, possiamo eliminare gli altri due nella riga. Se però
eliminiamo il 6 in I9, deve forzatamente essere giusto quello in I4, o la
colonna rimarrà senza sei.
Se questo è giusto, però, dobbiamo eliminare l’altro 6 nello stesso
riquadro, in H6. Se quest’ultimo viene eliminato, il 6 in C6 deve forzatamente
essere giusto, o non ci saranno 6 nella riga. Se il 6 in C6 è giusto, quello in
C3 deve essere eliminato.
Vediamo ora se ci sono numeri che risultano sbagliati in entrambe le nostre
possibili soluzioni. Potremo così eliminarli.
Ce ne sono due.
Qualunque sia il 6 giusto nella seconda riga, infatti, il 6 in C3 è per
forza sbagliato, perché abbiamo dimostrato che ha necessariamente un candidato
giusto nella sua colonna (in C2 o C6).
Anche il 6 in D9 è sbagliato (perché abbiamo dimostrato che sarà
forzatamente giusto o il candidato in I9 o quello in D2.)
Più semplicemente, i 6 in C3 e in D9 sono comunque sbagliati perché sono
indicati da una freccia nera in entrambi i nostri schemi.
In questo modo abbiamo escluso due candidati nelle caselle. Ci è costato un
bel po’ di fatica ma ora non siamo più bloccati!














Commenta via Facebook